Mechanical Springs Constant
Definition: The constant rate of force per a defined distance traveled of a mechanical spring made of helically wound round wire.
Mechanical springs consist of coils. The constant force these mechanical springs are able to exert through their coils is based upon the many physical dimensions and sometimes custom modifications the spring might have. There are different types of mechanical springs; mechanical compression springs,mechanical extension springs, mechanical torsional springs, and mechanical conical tapered springs. Mechanical cone springs do not exert a constant amount of force per distance traveled due to the variation in the outer diameters.
Mechanical Compression Springs:
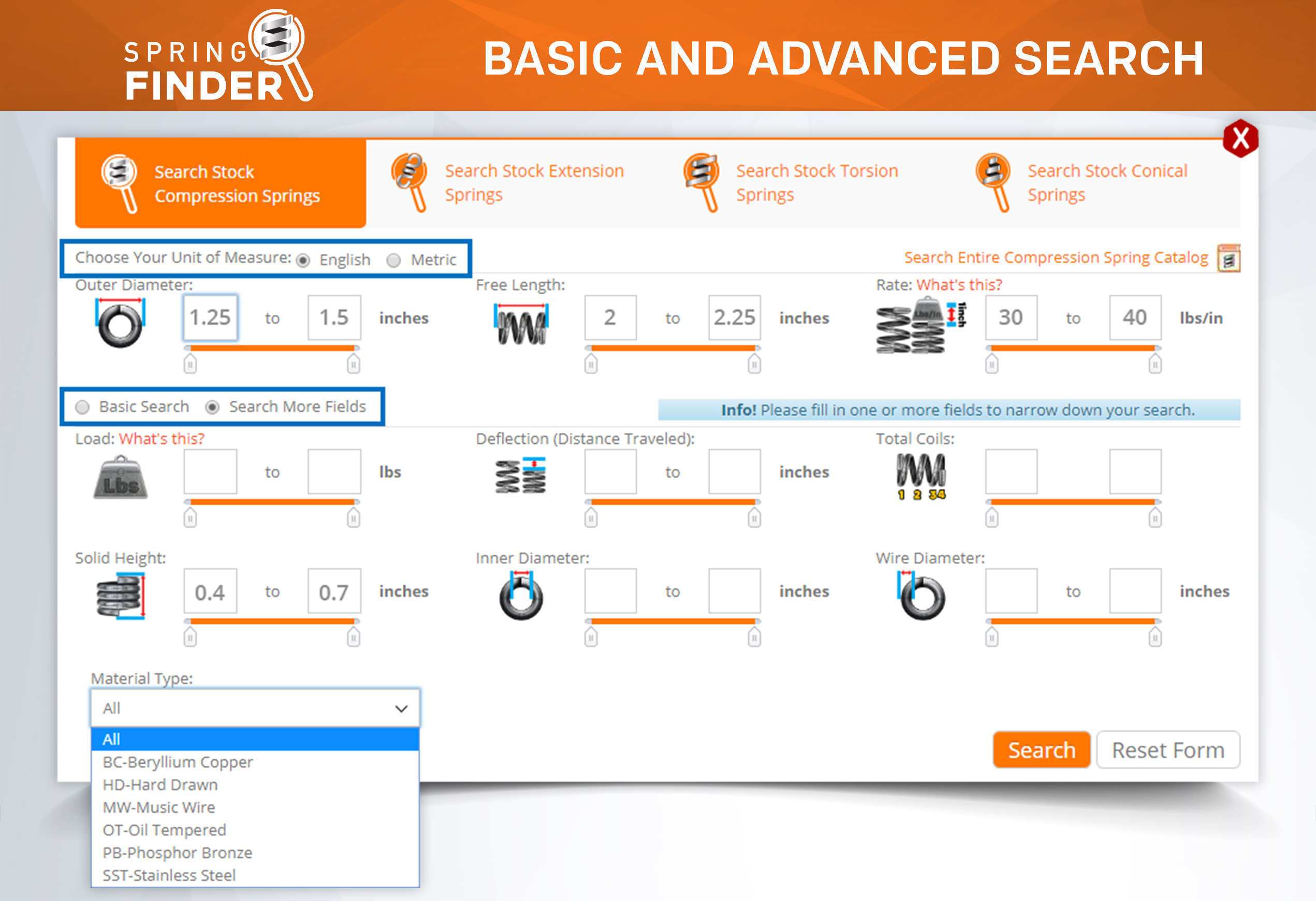
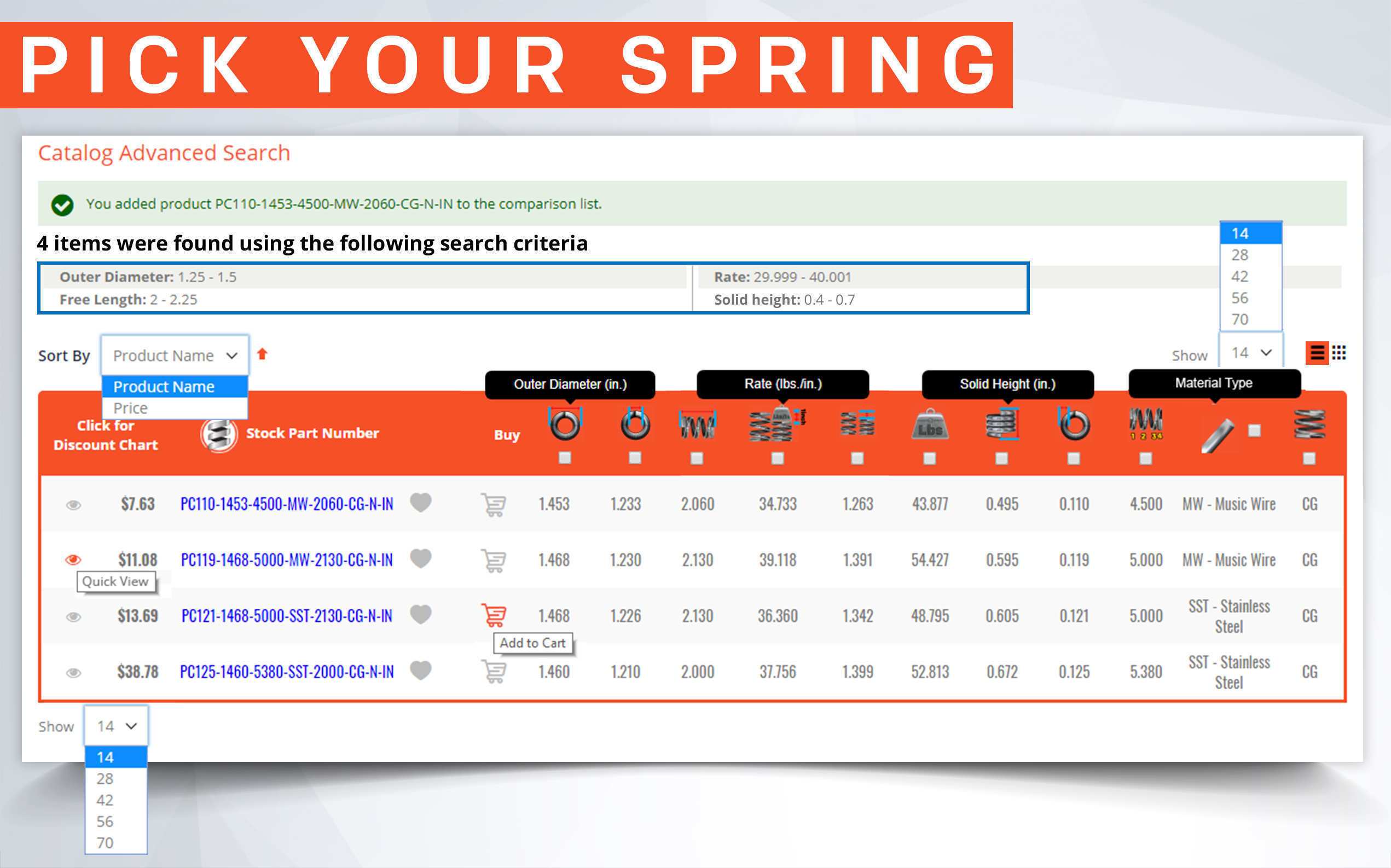
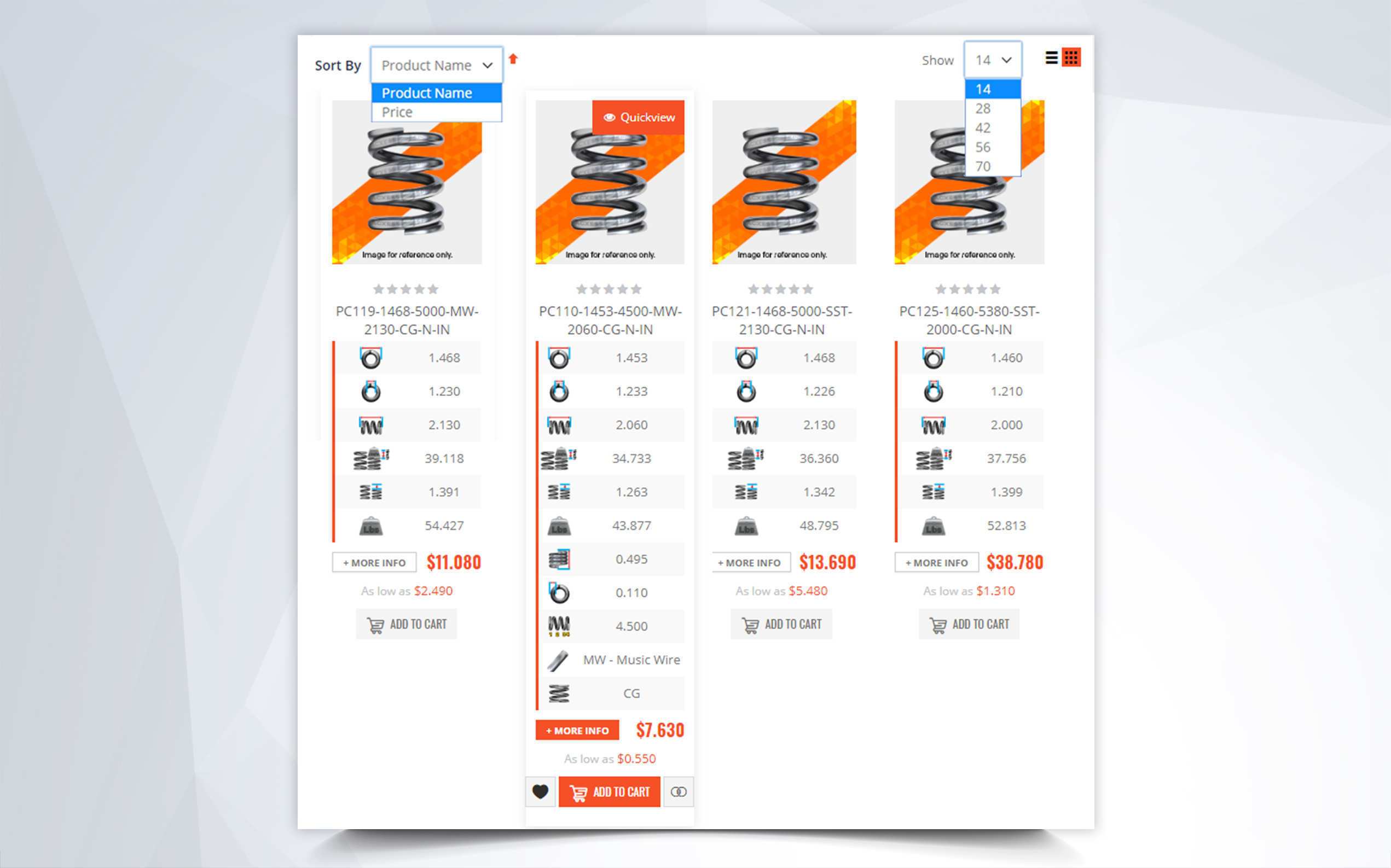
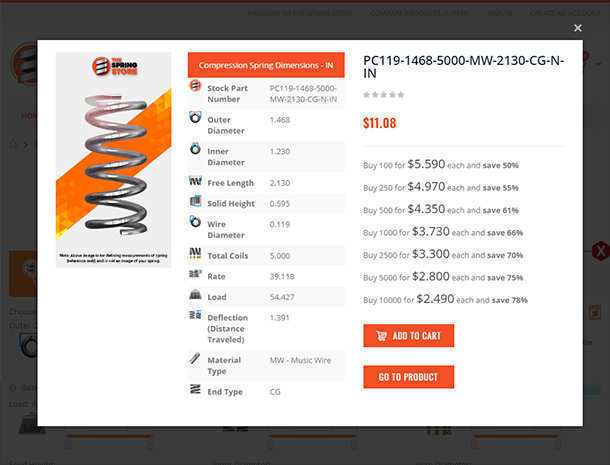
Mechanical compression springs have pitch in between the coils which make it possible for these to be compressed. Their force depends on the tightness of the coils' diameters and the amount of pitch in between these coils. If your mechanical compression spring has many coils and little pitch in between them, there is a chance that it will compress down to its solid height depending on the spring index (tightness of the coils). If it has very little coils with a lot of pitch in between them, the mechanical spring will be very strong but, due to the stress in between its coils and the tightness of the diameter, it might not be able to deflect to its solid height without taking a permanent set. The spring constant of mechanical compression springs is defined as pounds of force per inch (newtons per millimeter). It is calculated by dividing the required load you will be applying on the spring by the amount of travel it should deflect to reach your desired loaded height as shown in the formula below.
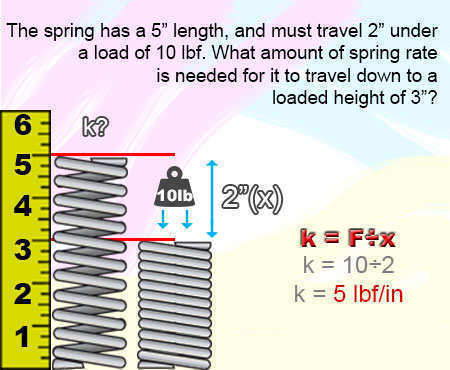
Rate (k) = Load (F) ÷ Travel (x) k = F ÷ xIf your spring will travel 2" (inches) under a load of 10lbf (pounds of force), the spring rate will be of 5lbf/in (pounds of force per inch).
k = F ÷ x k = 10 ÷ 2 k = 5Example 1.)
Mechanical Extension Springs:
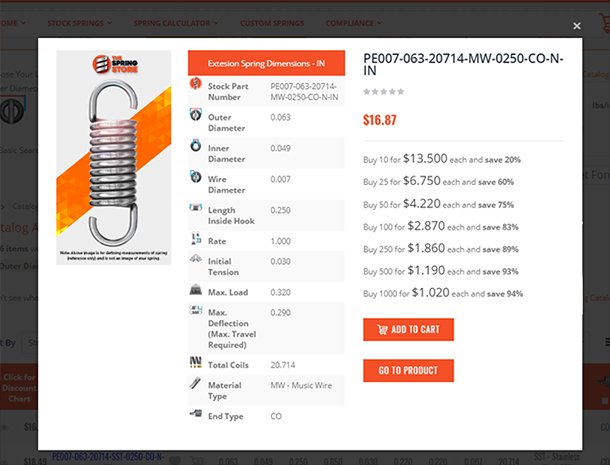
Mechanical extension springs don't have any pitch in between its coils. They are made by tightly winding the coils one on top of the other to be able to exert an amount of force when it is being extended. They are manufactured with hooks on the ends which latch on to the pieces in the mechanism that will be pulling on the spring. The force of your spring also depends on the spring index and the amount of coils. In this case, the amount of coils is based on the spring's body length (length of spring without the hooks) and the wire diameter. The less coils your spring has and the tighter the spring index is, the more force and stress it will have. Meaning that it will be a strong spring but it will not be able to deflect much. In between the coils there is already a stored energy which is released once the extension spring is extended to a point where light shows in between its coils. This is the tension that allows for your spring's coils to be fully compressed. The initial tension is an additional force besides the one based on your spring rate. This means that to calculate a mechanical extension spring's rate, you will need to subtract the initial tension from the load and then divide the result by the amount of traveled distance required to meet an extended length as shown in the following formula.
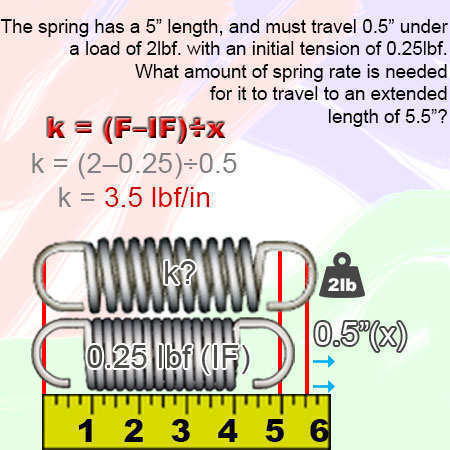
Rate [k] = (Load [F] – Initial Tension [IF]) ÷ Travel [x] k = (F – IF) ÷ xIf your spring is required to travel 0.5" (inches) under a load of 2lbf (pounds of force) and has an initial tension of 0.5lbf (pounds of force), the spring rate will be of 0.875lbf/in (pounds of force per inch).
k = (F – IF) ÷ x k = (2 – 0.5) ÷ 0.5 k = 1.5 ÷ 0.5 k = 3.5Example 2.)
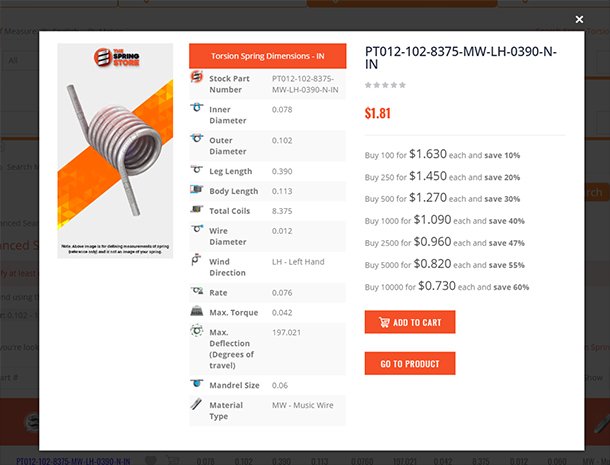
Mechanical Torsion Springs:
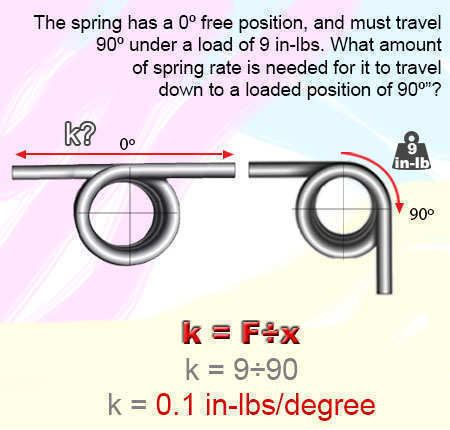
Mechanical torsion springs also don't have any pitch in between the coils like mechanical extension springs do but these execute a radial force instead of a linear one like both extension and compression springs do. The way to know a mechanical torsion spring from a mechanical extension spring is the difference in the ends. Mechanical torsion springs have legs which help it torque inside a mechanism while mechanical extension springs have hooks to be pulled or extended. For torsional springs, the same rule applies for more and less force as it does to compression and extension springs. More coils generate less force while tight spring indexes generate more force and vice versa. To calculate the constant force of a mechanical torsion spring the units of measurement change from pounds of force to inch-pounds of force; and the units for travel change from inches to degrees of deflection due to this being a rotational force. We calculate the rate per degree by dividing the amount of force by the required degrees of travel as shown in the formula below.
Rate per Degree (k) = Torque (T) ÷ Deflection (x) k = T ÷ x If your spring will be traveling 90º (degrees) of deflection under a load of 9 inch-pounds, the rate per degree is of 0.1 in-lbs/deg. (inch-pounds per degree). k = T ÷ x k = 9 ÷ 90 k = 0.1Example 3.)